title profile picture

0x530x650x610x6E

기울기 벡터를 이용한 응용 문제 풀이.

Jan 22, 2021
·

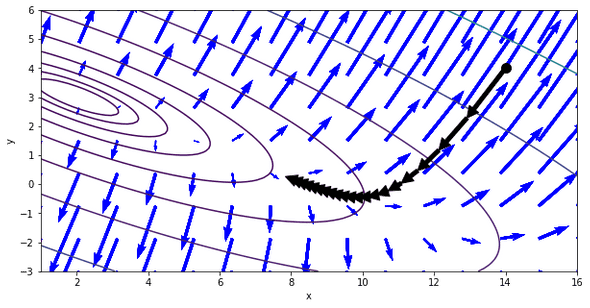
함수 f(x,y) = 2x2+6xy+7y2−26x−54y+1072x^2 + 6xy + 7y^2 -26x -54y + 107로 표현되는 지형을 그래프로 나타내고, 지형의 (14,4)지점에 공을 두었다면 어떤 경로로 공이 움직일지 경로를 그려라

import matplotlib.pyplot as plt
import numpy as np
import sympy
import matplotlib as mpl
import scipy as sp
import pandas as pd
black = {'facecolor':'black'}
def f(x,y):
    return 2*x**2+6*x*y+7*y**2-26*x-54*y+107
xx = np.linspace(1,16,100)
yy = np.linspace(-3,6,90)
X, Y = np.meshgrid(xx,yy)
Z=f(X,Y)

def gx(x,y):
    return 4*x+6*y-26
def gy(x,y):
    return 6*x+14*y-54

xx2 = np.linspace(1,16,15)
yy2 = np.linspace(-3,6,9)
X2,Y2 = np.meshgrid(xx2,yy2)
GX = gx(X2,Y2)
GY = gy(X2,Y2)
plt.figure(figsize=(10,5))
plt.contour(X,Y,Z, levels=np.logspace(0,3,10))

x0=(14,4)
plt.plot(x0[0],x0[1],'ko',ms=10)

for i in range(20):
    g=np.array((gx(x0[0],x0[1]),gy(x0[0],x0[1])))
    x_next= x0-0.02*g
    plt.annotate('',xy=x_next,xytext=x0,arrowprops=black)
    x0= x_next
    plt.quiver(X2,Y2,GX,GY,color='blue', scale=400, minshaft=2)

plt.xlabel('x')
plt.ylabel('y')

plt.show()

png